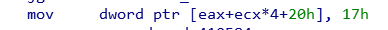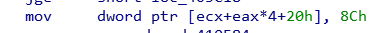NEWS

新闻资讯

首页 >> 技术资讯 >>技术分享 >> 软件常用加密算法并简单逆向识别知识
详细内容

软件常用加密算法并简单逆向识别知识

前言

想作为分析勒索病毒前的密码学接触.有些太难的算法,弟弟属实吃力,就不献丑了.可能也存在未察觉的错误,希望各位帮忙提出来,避免误导他人.谢谢师傅们.

 

常用加解密算法的逆向分析中的识别,不做过多算法原理上的叙述,别人讲的好多了.站在巨人的肩膀上.

 

这篇文章只作为特征查找用来辅助平时分析用.

 

两种工具ida插件FindCrypt2和peid的KANA进行算法识别是很好用的.

Base64

历史发展

base64最早就是用来邮件传输协议中的，原因是邮件传输协议只支持 ascii 字符传递，因此如果要传输二进制文件，如：图片、视频是无法实现的。因此 base64就可以用来将二进制文件内容编码为只包含 ascii 字符的内容，这样就可以传输了.

 

简单来说为了兼容各种数据格式.

基本原理

采用每三字节置换为四字节的方式,3x824位二进制转换为4x6的方式,前两位用0填充.字符不够转换的话,空字符=填充.(1字节或二字节输入,那么只能使用输出的2个或3个字符)

 

使用字符表"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"置换

 

Base24:"BCDFGHJKMPQmogRTVWXY2346789"

 

Base32:"ABCDEFGHJKLMNOPQRSTUVWXYZ234567"

 

Base60:"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwx"

逆向初探

Findcrypt2和KANAL都能是识别出置换表.

 

所以先关注置换表,然后关注下相关的位运算操作,可能就是base相关算法.

 

编码伪代码部分:image.png

魔改Base64

  1. 置换表里的字符顺序变化或者修改置换表
  2. 将置换表分成几个不连续的部分,根据偏移进行对应的索取,或者进行加密.

嘛 具体问题具体分析

单向散列

用的比较多的就是MD5和SHA-1等算法

MD5

特征

这里和加密与解密上都讲的挺好的,我做些我需要的东西的提炼

 

img

  1. 填充消息使其长度与448 mod 512同余,是为了后面填充64位的长度.

    填充方法:附一个1在消息后面,然后用0填充,填充长度0<x<=512

  2. 初始化最开始需要使用0x67452301,0xefcdab89,0x98badcfe,0x10325476进行初始化

  3. 然后进行数据处理,相关细节看书和源码就好.需要使用左移数组{ 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7,12, 17, 22, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20,4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 6, 10,15, 21, 6, 10, 15, 21, 6, 10, 15, 21,, 6, 10, 15, 21 }和

    64个存放32位字节的加法常数数组,由2^32 * (abs(sin(i)))得出,i的范围1到64.

    { 0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8, 0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70, 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 };

  4. 1
    2
    3
    4
    #define F(x, y, z) (((x) & (y)) | ((~(x)) & (z))) 
    #define G(x, y, z) (((x) & (z)) | ((y) & (~(z)))) 
    #define H(x, y, z) ((x) ^ (y) ^ (z)) 
    #define I(x, y, z) ((y) ^ ((x) | (~(z))))

  5. 512位消息分组为16组 x 32位,进行4*16次运算

  6. 128位散列值。

逆向识别

FindCrypt2和peid的KANA都是识别加法常数

 

采用加密与解密中的MD5KeyGen.exe进行分析学习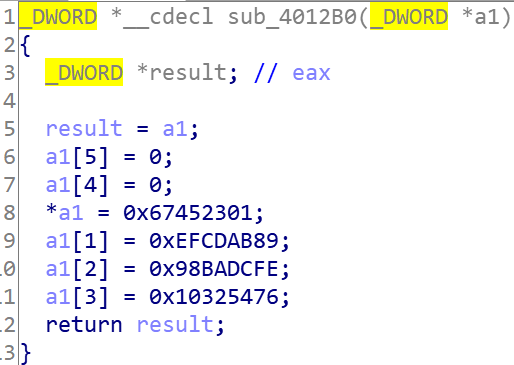

  1. image.png寄存器初始化

  2. MD5计算部分伪代码image.png

    每使用16个硬编码常量,都会发现算法的改变.详细算法看上面第四点

  3. 这样简单的确定了是MD5算法,然后可以从image.png进行回溯,ida识别有点问题,汇编看了下二者相等.

  4. image.png

    v11是置换表说明v4可能就是计算后的值,再动态调试可知,过滤掉前面的判断进行MD5计算的值为image.png

    说明在中途加了www.pediy.com字符串,

  5. image.png

    sub_4012E0集成了字符串添加和拷贝的字符大小刚好等于原字符串差64位的大小时,拷贝并直接计算MD5的功能.

    image.png

  6. 大概的流程差不多分析出来了,基本上修改下原版MD5的算法就能写出注册机了

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    #!python3
    import hashlib
    str  = input()
    str +='www.pediy.com'
    hash = hashlib.md5()
    hash.update(str.encode('utf-8'))
    hash = hash.hexdigest()
    code = "23456789ABCDEFGHJKLMNPQRSTUVWXYZ"
    serial = ""
    for i in range(0,len(hash),2):
        a = '0x' + hash[i]+hash[i+1]
        serial = serial+code[eval(a)%32]
    serial = serial[:4] + '-' + serial[4:8] +'-' + serial[8:12] +'-'+serial[12:16]
    print(serial)

    image.png

魔改

  1. 可能会改变四个常数
  2. 改变输入后的字符,添加或者做某些运算等等
  3. hash处理过程可能改变

SHA算法

散列值长度:SHA-1 160位 SHA-256256位 SHA-384 384位 SHA-512512位

 

SHA-2包括SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256

SHA-1

原理参考:https://www.wosign.com/News/news_2018121101.htm 讲的很详细

特征

  1. 消息填充和MD5一样,512位为一组,然后16组x32位,然后扩充位80组x32位,进行4*20次运算

  2. 使用该函数进行计算A,B,C,D,E←[(A<<5)+ ft(B,C,D)+E+Wt+Kt],A,(B<<30),C,D,f函数伪代码在下方

    1
    2
    3
    4
    #define F0(x,y,z) ((x&y)|((~x)&z))
    #define F1(x,y,z) (x^y^z)
    #define F2(x,y,z) ((x&y) | (x&z)|(y&z))
    #define F3(x,y,z) (x^y^z)

  3. 使用常数

    1
    2
    3
    4
    #define K0 0x5a827999L
    #define K1 0x6ed9eba1L
    #define K2 0x8f1bbcdcL
    #define K3 0xca62c1d6L

    初始化寄存器的hash值

    1
    2
    3
    4
    5
    #define H0 0x67452301L
    #define H1 0xefcdab89L
    #define H2 0x98badcfeL
    #define H3 0x10325476L
    #define H4 0xc3d2e1f0L

逆向初探SHA-1加密

使用加密与解密的6.1.2示例程序

  1. FindCrypt插件识别出SHA-1常量

    image.png

  2. 对输入进行判断,Name不为空,Serial为20位

    image.png

  3. 基本流程image.png

  4. 注册机

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    #!python3
    import hashlib
    output = []
    str = input()
    hash = hashlib.sha1()
    hash.update(str.encode('utf-8'))
    hash = hash.hexdigest()
    xor_str_1 = [0x50,0x45, 0x44, 0x49, 0x59, 0x20, 0x46, 0x6F ,0x72 ,0x75, 0x6D, 0x00 ]
    xor_str_2 = "pediy.com"
    num = 0
    # print(hash)
    for i in range(0,34,2):
        if i > 22:
            b = '0x' + (hash[i] + hash [i+1])
            a = eval(b) ^ eval(output[int((i/2))-12])
            output.append(hex(a))
            continue
        b = '0x' + (hash[i] + hash [i+1])
        a = eval(b) ^ (xor_str_1[int(i/2)])
        output.append(hex(a))
     
    for i in range(34,40,2):
        b = '0x' + (hash[i] + hash [i+1])
        a = eval(b) ^ ord(xor_str_2[int(i/2)-17])
        output.append(hex(a))
    for i in range(10):
        output[10+i] = hex(eval(output[i]) ^ eval(output[10+i]))
     
    for i in range(10,20):
        print('{:0>2}'.format((output[i][2:]).upper()),end = "")

    成功image.png

  5. 计算函数的部分伪代码参考image.png

总结

要注意字节与位转换函数,不太熟悉容易迷惑

1
2
3
4
for (i=0;i<20;i++)
{ /* convert to bytes */
    hash[i]=((sh->h[i/4]>>(8*(3-i%4))) & 0xffL);
}

对称加密

RC4

RC4生成一种被称为密钥流的伪随机流.它与加密的数据长度相等.密钥流与数据同位异或进行加解密.密钥流生成分为两个部分KSA与PRGA.

  1. the key-scheduling Algorithm (KSA) 密钥调度算法

    按照升序0,1,2,3,4.....,254,255初始化一个256字节数组S.

    使用密钥填充一个256字节数组T ,长度不够的话,轮转填入,直到填满.

    对数组S进行打乱.

    int j = 0;
for (i = 0;i<256;i++){
    j =(j+S[i]+T[i])%256;
    swap(S[i],S[j]);
}

  2. the Pseudo-Random Generation Algorithm (PRGA) 伪随机生成算法

    int i, j = 0;
while (data_length--) {
i = (i + 1) % 256;
i = (i + 1) % 256;
j = (j + S[i]) % 256;
swap(S[i], S[j]);
int t = (S[i] + S[j]) % 256;
int k = S[t];
//k为加密密钥,直接进行与数据异或或者存进数组里最后进行异或都可以,
}

  3. 函数完整代码

    #include<iostream>
using namespace std;

int S[256] = { 0 };

void swap(int& a, int& b) {
    int c = a;
    a = b;
    b = c;
}
void KSA(unsigned char key[], int len) {
    for (size_t i = 0; i < 256; i++) S[i] = i;
    int j = 0;
    for (size_t i = 0; i < 256; i++)
    {
        j = (j + S[i] + key[i % len]) % 256;
        swap(S[i], S[j]);
    }
}
void PRGA(unsigned char data[], int len) {
    int i = 0, j = 0, num = 0;
    int data_length = len;
    while (data_length--) {
        i = (i + 1) % 256;
        j = (j + S[i]) % 256;
        swap(S[i], S[j]);
        int t = (S[i] + S[j]) % 256;
        int k = S[t];
        data[num] = (data[num] ^ k);
        num++;
    }
}

int main() {
    unsigned char key[] = "xwdidi.com";
    unsigned char data[] = "bbspediycom";
    KSA(key, strlen((char*)key));
    PRGA(data,strlen((char*)data));
    for (size_t i = 0; i < strlen((char*)data); i++)
    {
        cout << hex << (int)data[i] << " ";
    }
    return 0;
}

初探逆向识别RC4

使用加密与解密中的RC4Sample进行分析学习.

主函数体伪代码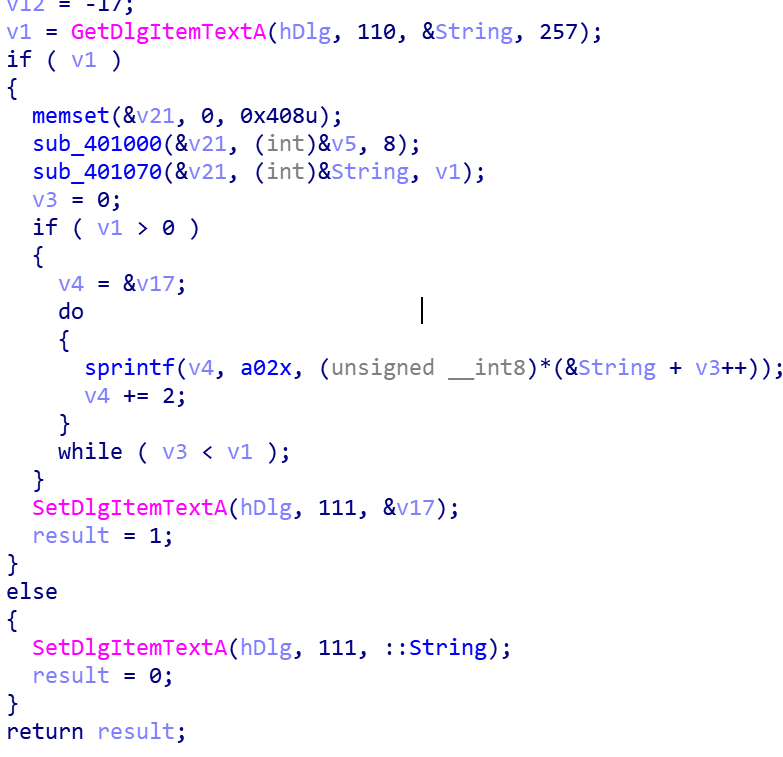

image.png中间两个函数可能就是KSA和PGRA.

sub_401000

伪代码全图:image.png

 

可以看中间do-while循环,有一个数组的256位初始化.说明a1+2是一个数组s-box的位置,那么*a1和a1[0]就是两个int型变量.然后下面的循环中,其实是交换和计算j是交叉在一起的.31,32,35,36是计算j的位置,30,33,34是交换.

 

通过v3与a3比较,获得对key长度取余的效果.v8则是每循环一次加一取值的s-box.

sub_401070

image.png

 

第一眼会发现做了异或操作,可能这就是PRGA.

 

仔细观察后发现result[2]其实是s-box的首地址,其他变量的话就是相对首地址的偏移.30,31,34,35,36其实交换函数.其他就是获得异或key所需的偏移计算.

魔改RC4

  1. 使用其它算法对参数进行加密,与其他加密算法糅合.
  2. S盒的内部数据固定

总结

对于循环,又有256或者0x100的关键字,获取字符串长度,又再次使用处理过的值进行异或的话可以去怀疑是RC4加密.

TEA

xtea,xxtea,tea都可以用0x9E3779B9识别,详细分析后面有空再写吧

AES

基本原理

分组长度:128比特

 

密钥长度:128, 192, 256比特

 

圈数:分别为10, 12, 14

 

设定Nr为第r+1次轮函数. 将输入复制到状态数组中.在进行一个初始轮密钥加操作之后, 执行Nr次论函数.对状态数组进行变换, 其中最后一轮不同于前Nr-1 轮. 将最终的状态数组复制到输出数组中. 即得到最终密文(引用自加密与解密)

 

AES-128: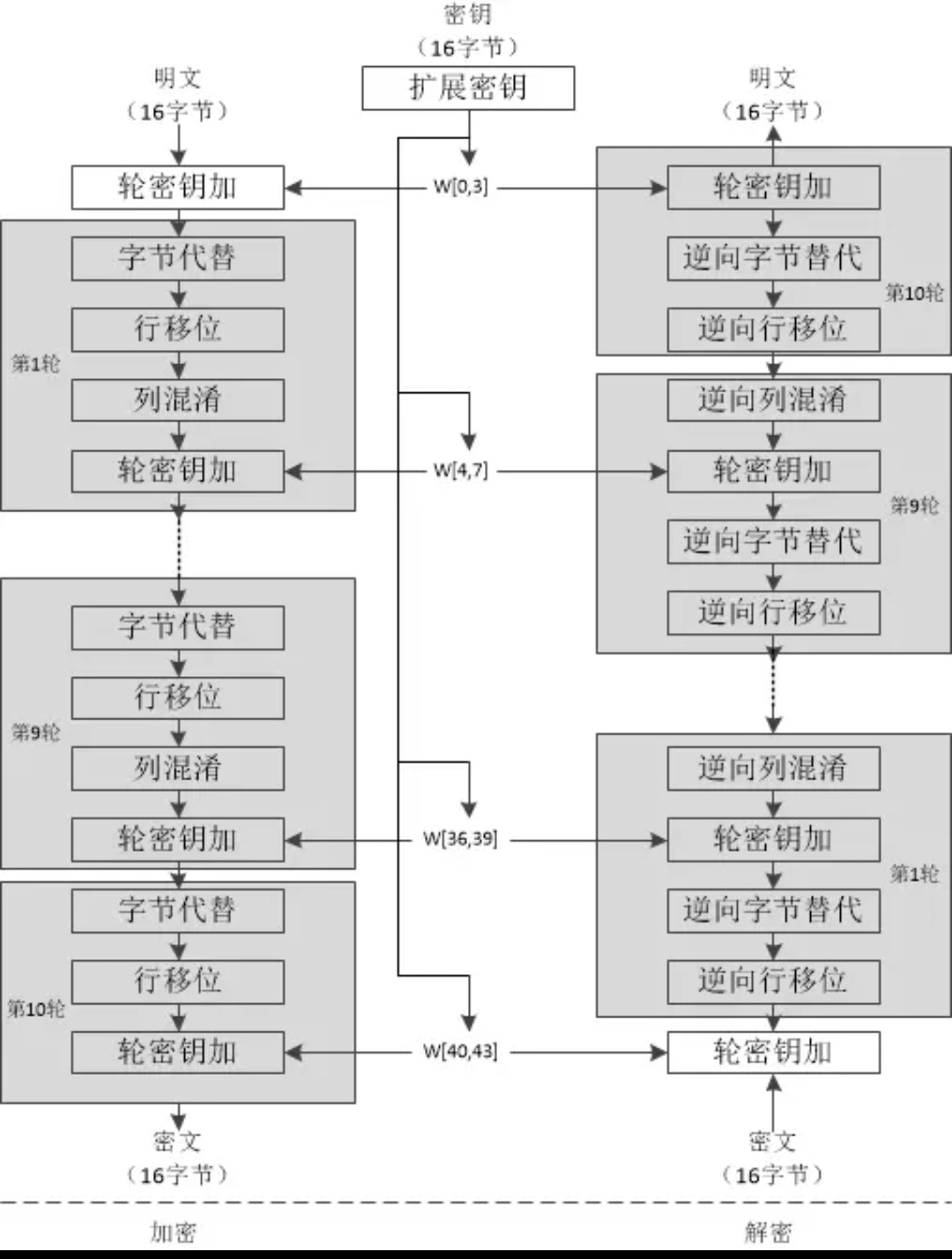

 

Screenshot_20191122_193156.jpg

 

轮密钥加(AddRoundKey):将状态元素与轮密钥进行简单的异或计算,唯一需要三个参数的过程.

 

字节替代(SubBytes):使用S-box进行查表,字节替换操作。

 

S-box:

 

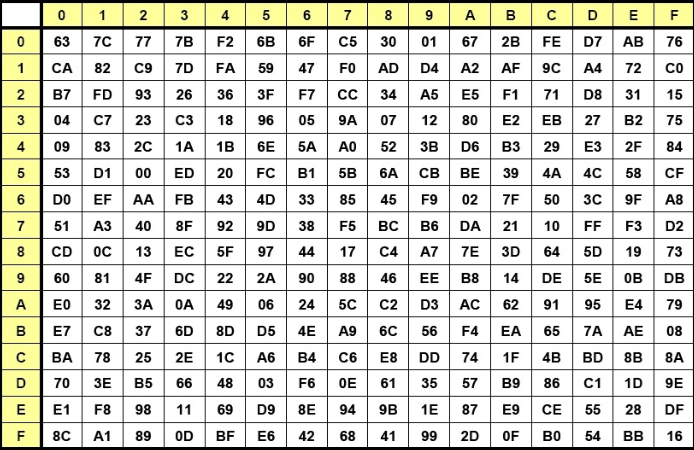
image.png

 

行位移(ShiftRows):数组大小为4x4字节,第一行保持不变,第二行循环左移1字节,第三行循环左移2字节,第四行循环左移3字节.

 

列混淆(MixColumns):以列为单位,可看作进行矩阵乘法,矩阵为((02,03,01,01)(01,02,03,01)(01,01,02,03)(03,01,01,02))

 

密钥扩展(KeyExpansion):通过密码扩展算法生成Nr+1个32位双字

 

解密就是逆过程了

空间换时间

大多数时候,常见aes使用空间换时间

 

将轮函数的几个步骤合并为一组简单的查表操作,只是最后一步没有,需要使用常规方法处理.

 

然后需要4个T表，一个T表需要256个4字节的32位双字，所以需要4kb的存储空间.

 

每进行一轮,4次查表,4轮异或运算.一共有四次,16轮查表,16轮异或

 

T表数据图

 

img

1
2
3
4
t0 = Te0[s0 >> 24] ^ Te1[(s1 >> 16) & 0xff] ^ Te2[(s2 >> 8) & 0xff] ^ Te3[s3 & 0xff] ^ rk[round*4];
t1 = Te0[s1 >> 24] ^ Te1[(s2 >> 16) & 0xff] ^ Te2[(s3 >> 8) & 0xff] ^ Te3[s0 & 0xff] ^ rk[round*4+1];
t2 = Te0[s2 >> 24] ^ Te1[(s3 >> 16) & 0xff] ^ Te2[(s0 >> 8) & 0xff] ^ Te3[s1 & 0xff] ^ rk[round*4+2];
t3 = Te0[s3 >> 24] ^ Te1[(s0 >> 16) & 0xff] ^ Te2[(s1 >> 8) & 0xff] ^ Te3[s2 & 0xff] ^ rk[round*4+3];

逆向初探识别RSA

一样使用的是加密与解密中的样例

  1. FindCrypt识别处MD5和AES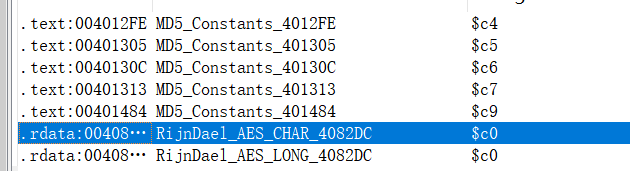image.png

  2. Serial长度为32字节，使用16进制的话刚好为128位。image.png

  3. 静态分析大概这样，接下来动态看看image.png

  4. sub_401320压入初始化后的寄存器数组地址，name, 长度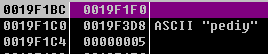image.png

  5. 最终获得128位MD5散列值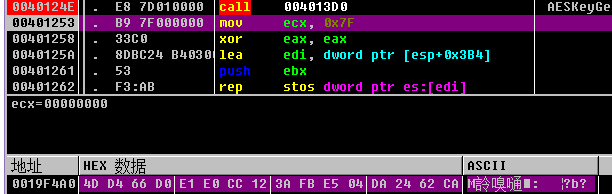image.png

  6. 执行sub_401EC0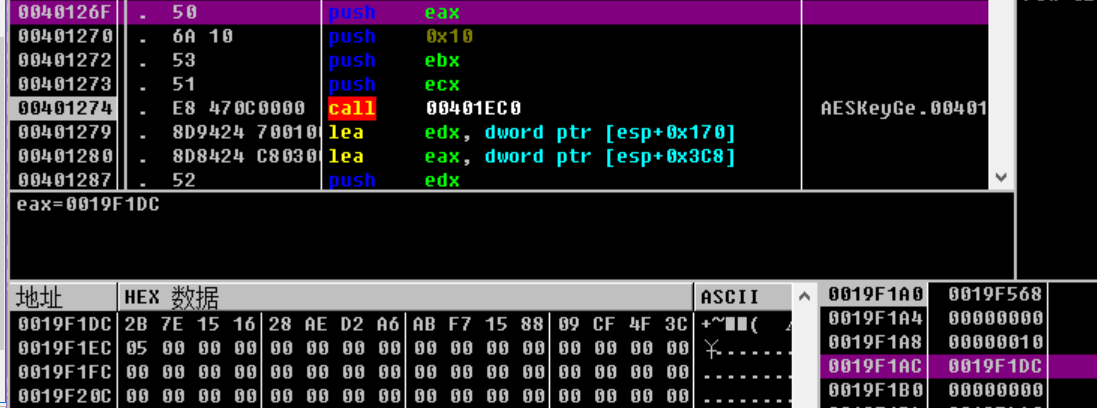

  7. 内存中的sbox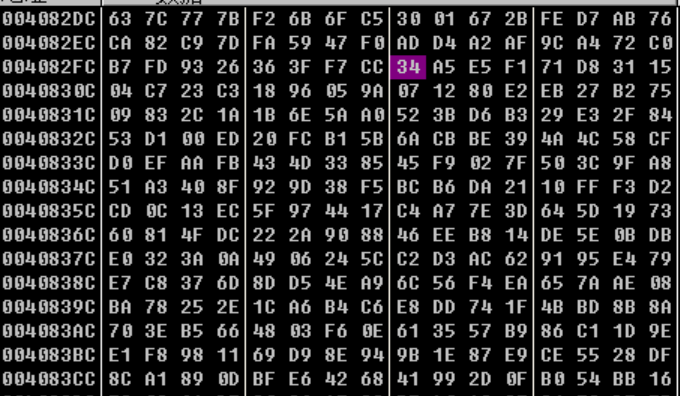

    image.png

  8. 细致算法省略

    image.png函数中存在大量的移位异或操作,太大了就不截图了.

  9. 注册机

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    #!python3
    from Crypto.Cipher import AES
    import hashlib
    #"xwdidi" md5
    hash = b"\x39\xd7\x8e\xe5\x67\xf3\xf2\x96\xad\x84\x8d\x3f\xcd\xb1\xd4\x61"
    key = b"\x2b\x7e\x15\x16\x28\xae\xd2\xa6\xab\xf7\x15\x88\x09\xcf\x4f\x3c"
    cipher = AES.new(key,AES.MODE_ECB)
    plaintext = cipher.decrypt(hash)
    for i in plaintext:
        print(hex(i)[2:].upper(),end="")

加密模式与填充模式

  • ECB: 需要加密的消息按照块密码的块大小被分为数个块，并对每个块进行独立加密。
  • CBC : 每 个明文块先与前一个密文块进行异或后，再进行加密
  • CTR
  • OCF
  • CFB

ECB 与 CBC

  • PKCS7Padding: 假设数据长度需要填充n(n>0)个字节才对齐，那么填充n个字节，每个字节都是n;如果数据本身就已经对齐了，则填充一块长度为块大小的数据，每个字节都是块大小。

  • PKCS5Padding:PKCS7Padding的子集，块大小固定为8字节

  • Zero-Padding 用0填充(适合以\ 0结尾的字符串加解密)

非堆对称加密

RSA

基本原理

  1. 选择两个不同大的质数p和q,计算n=p*q

  2. 根据欧拉函数,求得r=φ(n)=φ(p)φ(q)=(p−1)(q−1)

  3. 选择一个与e互质且小于r的整数,并求得c关于r的模反元素,命名为d,有ed ≡ 1 mod r

  4. 销毁p和q,此时(n,e)为公钥,(n,d)为私钥

  5. $$
    加密
    加密 n^e ≡ c \bmod N,消息解密c^d ≡ n \bmod N \
    (只需要证明n^{ed} ≡n\bmod N即可)
    $$

逆向初探RSA

发现这个程序和书前文使用Miracl库运算的逻辑相同,那也简单分析一下.

 

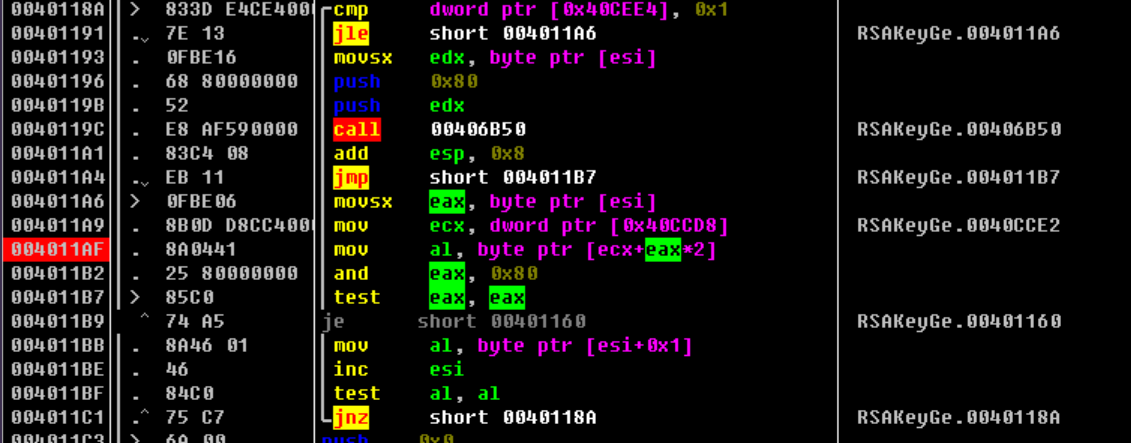
image.png

  1. image.png

    逐一检测数据是否为0123456789abcdeABCDEF中的数据,如果有则直接报错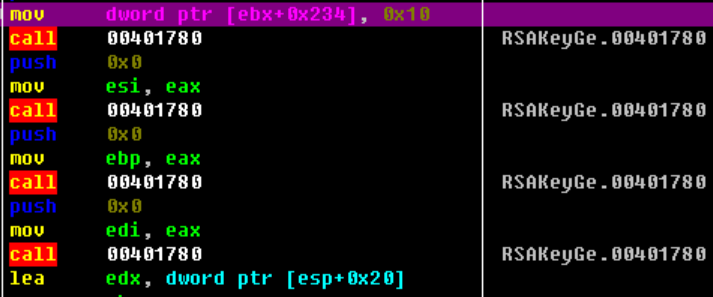

  2. image.png

    参数初始化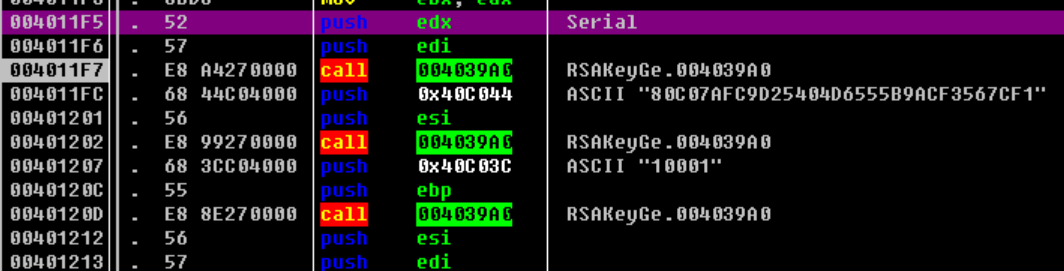

  3. image.png

    传入Serial赋值m,大数n和e

  4. image.png

    计算取模

  5. image.png

    比较判断是否正确

  6. 由此我们可知是将serial进行RSA解密与输入进行比较.得知了n=0x80C07AFC9D25404D6555B9ACF3567CF1和e=0x10001

  7. 使用大数分解RSATool的Factor N功能,得到p=0xA554665CC62120D3,q=0xC75CB54BEDFA30AB

  8. 输入E,点击Calc. D得到d=0x651A40B9739117EF505DBC33EB8F442D

  9. xwdidi的16进制为787764696469,使用大叔计算器进行c ^d ≡ m mod N计算,最后得到m=0x5D99FFF7B67285275C8639BCEF982B7 ,带入软件后返回Success!

  10. 注册机

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    #!python3
    import binascii
    c =input()
    a = ""
    for i in c:
        a = a + hex(ord(i))
    # print(a)
    a = a.replace("0x","")
    e = "0x" + a
    # print(e)
    result  =  pow(eval(e),0x651A40B9739117EF505DBC33EB8F442D,0x80C07AFC9D25404D6555B9ACF3567CF1)
    print(hex(result)[2:])

  11. powmod函数的部分伪代码作为参考image.png

Mircal大数运算库

Mircal库过于常用,需要进一步的熟悉才能更加利于分析.

 

头文件有mircal.h和mirdef.h两者,库文件为ms32.lib

 

以下是大数运算库函数的Magic number

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
MIRACL MAGIC NUMBERS TABLE:
                       by bLaCk-eye
        from an original ideea by bF!^k23
        Modified by cnbragon for miracl v5.01
 
NUMBER OF FUNCTIONS:    96h
 
innum                equ 01h .
otnum                equ 02h .
jack                equ 03h .
normalise            equ 04h .
multiply            equ 05h .
divide                equ 06h .
incr                equ 07h .
decr                equ 08h .
premult                equ 09h .
subdiv                equ 0Ah .
fdsize                equ 0Bh .
egcd                equ 0Ch .
cbase                equ 0Dh .
cinnum                equ 0Eh .
cotnum                equ 0Fh .
nroot                equ 10h .
power                equ 11h .
powmod                equ 12h .
bigdig                equ 13h .
bigrand                equ 14h .
nxprime                equ 15h .
isprime                equ 16h .
mirvar                equ 17h .
mad                    equ 18h    .
multi_inverse        equ 19h .
putdig                equ 1Ah .
add                    equ 1Bh .
subtract            equ 1Ch .
mirsys                equ 1Dh .
xgcd                equ 1Eh .
fpack                equ 1Fh .
dconv                equ 20h .
mr_shift            equ 21h .
mround                equ 22h .
fmul                equ 23h .
fdiv                equ 24h .
fadd                equ 25h .
fsub                equ 26h .
fcomp                equ 27h .
fconv                equ 28h .
frecip                equ 29h .
fpmul                equ 2Ah .
fincr                equ 2Bh .
;null entry
ftrunc                equ 2Dh .
frand                equ 2Eh .
sftbit                equ 2Fh .
build                equ 30h .
logb2                equ 31h .
expint                equ 32h .
fpower                equ 33h .
froot                equ 34h .
fpi                    equ 35h .
fexp                equ 36h .
flog                equ 37h .
fpowf                equ 38h .
ftan                equ 39h .
fatan                equ 3Ah .
fsin                equ 3Bh .
fasin                equ 3Ch .
fcos                equ 3Dh .
facos                equ 3Eh .
ftanh                equ 3Fh .
fatanh                equ 40h .
fsinh                equ 41h .
fasinh                equ 42h .
fcosh                equ 43h .
facosh                equ 44h .
flop                equ 45h .
gprime                equ 46h .
powltr                equ 47h .
fft_mult            equ 48h .
crt_init            equ 49h .
crt                    equ 4Ah .
otstr                equ 4Bh .
instr                equ 4Ch .
cotstr                equ 4Dh .
cinstr                equ 4Eh .
powmod2                equ 4Fh .
prepare_monty        equ 50h .
nres                equ 51h .
redc                equ 52h .
nres_modmult        equ 53h .
nres_powmod            equ 54h .
nres_moddiv            equ 55h .
nres_powltr            equ 56h .
divisible            equ 57h .
remain                equ 58h .
fmodulo                equ 59h .
nres_modadd            equ 5Ah .
nres_modsub            equ 5Bh .
nres_negate            equ 5Ch .
ecurve_init            equ 5Dh .
ecurve_add            equ 5Eh .
ecurve_mult            equ 5Fh .
epoint_init            equ 60h .
epoint_set            equ 61h .
epoint_get            equ 62h .
nres_powmod2        equ 63h .
nres_sqroot            equ 64h .
sqroot                equ 65h
nres_premult        equ 66h .
ecurve_mult2        equ 67h .
ecurve_sub            equ 68h .
trial_division        equ 69h .
nxsafeprime            equ 6Ah .
nres_lucas            equ 6Bh .
lucas                equ 6Ch .
brick_init            equ 6Dh .
pow_brick            equ 6Eh .
set_user_function    equ 6Fh .
nres_powmodn        equ 70h .
powmodn                equ 71h .
ecurve_multn        equ 72h .
ebrick_init            equ 73h .
mul_brick            equ 74h .
epoint_norm            equ 75h .
nres_multi_inverse    equ 76h .
;null entry
nres_dotprod        equ 78h .
epoint_negate        equ 79h .
ecurve_multi_add    equ 7Ah .
ecurve2_init        equ 7Bh .
epoint2_init        equ 7Ch
epoint2_set            equ 7Dh .
epoint2_norm        equ 7Eh .
epoint2_get            equ 7Fh .
epoint2_comp        equ 80h .
ecurve2_add            equ 81h .
epoint2_negate        equ 82h .
ecurve2_sub            equ 83h .
ecurve2_multi_add    equ 84h .
ecurve2_mult        equ 85h .
ecurve2_multn        equ 86h .
ecurve2_mult2        equ 87h .
ebrick2_init        equ 88h .
mul2_brick            equ 89h .
prepare_basis        equ 8Ah .
strong_bigrand        equ 8Bh .
bytes_to_big        equ 8Ch .
big_to_bytes        equ 8Dh .
set_io_buffer_size    equ 8Eh .
epoint_getxyz       equ 8Fh .
ecurve_double_add   equ 90h .
nres_double_inverse equ 91h .
double_inverse      equ 92h .
epoint_x            equ 93h .
hamming             equ 94h .
expb2               equ 95h .
bigbits             equ 96h .

反汇编识别

反汇编识别着重在于查看函数内部的mov doword ptr [eax+ecx*4+20], yy格式的反汇编代码,yy即为magic number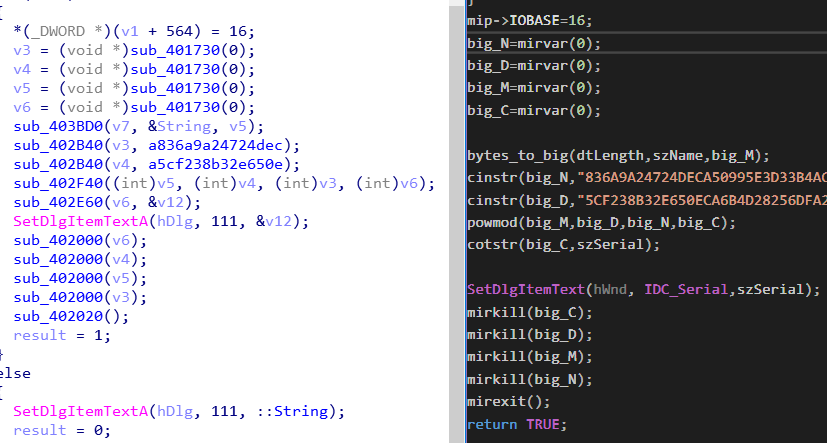

 

image.png

 

这是函数对比图

sub_401730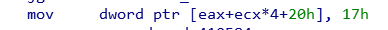

image.png

sub_403BD0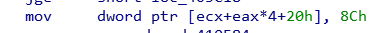

image.png

 

其他的就不一一找了,都在函数内部都能看见.基本上是这样去识别.

Reference

Phone:  132-6677-8242

E-mail:  528621124@qq.com

Adress:  深圳市龙岗区横岗街道

Copyright @ 2009 . All rights reserved.

客服中心
联系方式
132-6677-8242
153-6149-5056
- 技术咨询
点击这里给我发消息 点击这里给我发消息
扫一扫，微信咨询
seo seo